「発想の面白さ」を教えてくれた鳩の巣原理

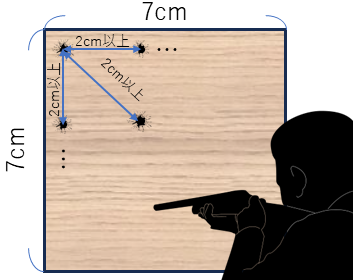
　「一辺が７cmの正方形の的がある。ここに50発の弾を銃で撃っていくとしよう。この時、どの２つの弾の跡をとってもその距離を2cm以上離すような撃ち方は存在するか？（弾やその跡の大きさは考慮しないものとする）」

　すべての二点ということなので、その二つのポイントの選び方は50C2、つまり1225通りある。それぞれが最短になるように実際に紙の上にプロットしていけばこれが可能かどうかのチェックというのは機械的にできないこともないだろう。
　今ならコンピュータで簡単に実験できるだろうし、しらみ潰しにやる方法というのはコンピュータなしでも実現可能だ。しかしこの方法は美しくない。

　このように考えてはどうだろうか。一辺が7cmということは、面積は49㎠となる。つまり、この正方形に縦横に１cm間隔で線を引いていくと、中に49個の一辺が1㎠の正方形ができることになる。
　ここに50個の点を打つわけだから、49個の正方形うち少なくとも最低１つには「２つ以上の点が含まれる」ことになる。（ここで大事なのは、最低、という点だ。別にそういう場所がもっとたくさんあってもいいし、綺麗に49箇所にわかれていてもいい。いずれにしても２個以上含む場所が最低一つはあることは確かである）。

　そうすると、その2点を含む正方形について考えた時、その中でその2点が最も離れた位置に置かれたとしてもそれは角と角、つまり対角線上ということになる。このときこの二つの距離は√２cmなので、2cmよりは短い。（√を習っていないという人は、もっとシンプルに考えてもよい。今一辺が１cmの直角二等辺三角形の一番長い辺を考えているわけだが、この辺の長さが他の2辺つまり1cm二つを足したものより大きくなるはずがない。もしそうなったらそれは三角形にはならないのだから）つまりはどんな置き方をしたとしても、最低一つは2cmよりも距離が短い場所が存在するということになる。
　これは、鳩の巣原理、あるいはディリクレの原理という考え方（関心のある方は調べてみてください）を用いた純粋に数学的、論理的な解答となっている。しらみ潰しにすべてをチェックしなくても、論理によって可能性をすべて網羅することができているわけだ。

数学の本質は計算ではない！　じゃあ創作の本質は？

　私はこの限定された中でどのように論理を展開するか、という点にある種のクリエイティブな魅力を感じている。例えば、曲をつくるときに「どんな曲でもいい」と言われたら、例えば長さが何時間もあって、音階の流れや、繰り返しもない、とにかく「何の調和も感じられない」音楽だって存在しうるわけだ。しかしそういったものを「優れた音楽だ」と感じることはあまり考えられないだろう。
　こういった条件の中で発想を展開させていくという点で数学は私の思うクリエイティブな魅力に富んでいる。
　ところで多くの人が数学を苦手だと感じているという事実もある。おそらくその原因のほとんどは「計算が苦手」ということにある。確かに学校における数学は計算が遅いだけでずいぶんとやりづらくなる。音楽で言えばそれは「楽器を上手く弾けるか」「楽譜を早く読めるか」ということに該当するように思う。当たり前だが、ほとんどの場合それは練習をしなければできるようにはならない（なかにはあまり練習をやらなくても最初からある程度できる人が稀にいるというところも一致している）。
　しかし例えば計算機や、サンプリング、打ち込みがそれを代替し、これからはAIがそうであるように、そういった部分は実は数学や音楽の必ずしも本質ではない。もちろん、楽器や計算はできた方が楽しいのだが、上記の問題で特に計算らしい計算がなく、論理の展開と発想で十分に「クリエイティブに」なれるということもわかると思う。
音楽や創作にも、もちろん単純作業的な部分も必要ではあるが、何かを思いついて、それをまず一つの形にしていくような瞬間がやはり醍醐味ではないだろうか。

連載をはじめから読む